Découvrir le sens des symboles = et ≠,
Comprendre et exprimer des situations de déplacement par des additions et soustractions,
Comprendre et exprimer des situations d’ajouts et retraits par des additions et soustractions,
Comprendre et exprimer des situations de tout et parties par des additions et soustractions,
Résoudre des problèmes mathématiques en reconnaissant la situation problème et en utilisant la bonne opération.
L’objectif principal est de faire découvrir l’addition et la soustraction comme 2 opérations mathématiques qui permettent de « raconter des histoires mathématiques » et donc de résoudre des problèmes mathématiques.
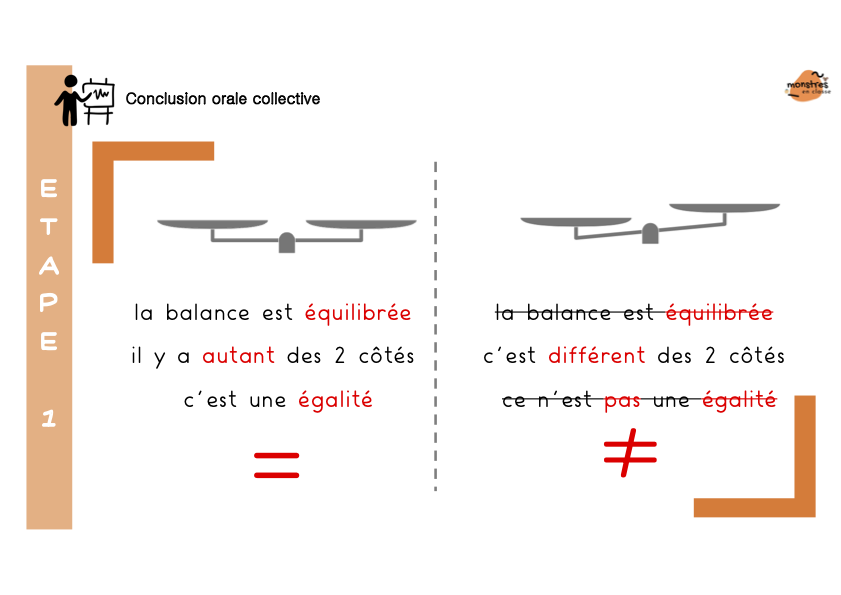
Dans un 1er temps, je présente les symboles = et ≠, et explique ce qu’est une égalité. Le symbole = n’est pas vu comme le signe d’un résultat mais bien comme le signe que les deux côtés de l’égalité représentent une valeur équivalente.
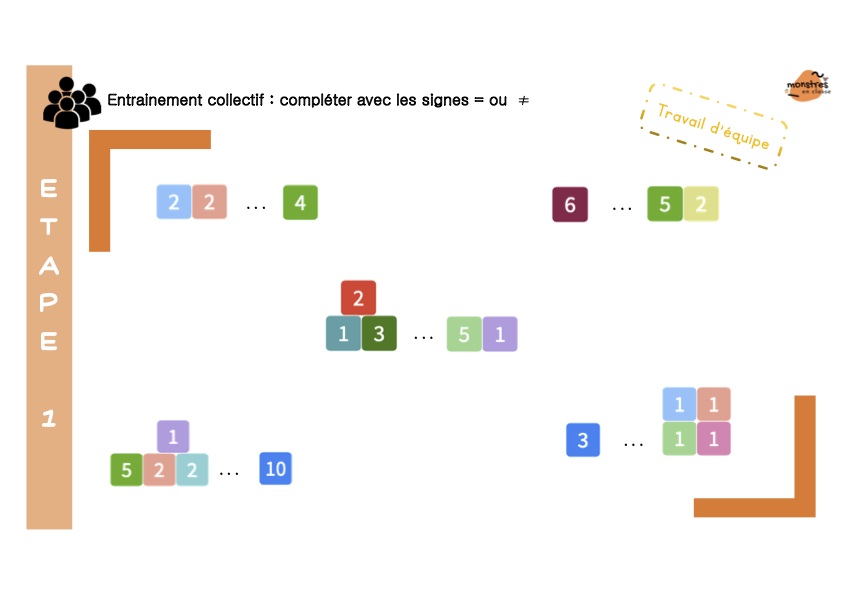
Ensuite, je présente les « histoires de déplacements en avant et en arrière », et j’introduis l’addition et la soustraction comme des opérations qui permettent de traduire en langage mathématique ces situations.
L’objectif est ici de présenter les 2 opérations en même temps, ainsi on ne donne pas de priorité à l’une ou l’autre, on ne prend pas le risque que les élèves s’habituent et privilégient l’addition car elle aura été abordée avant.
De plus, les opérations ainsi présentées sont comprises comme équivalentes : « avec l’addition, on avance, avec la soustraction, on recule. »
Les élèves commencent donc à résoudre des problèmes de déplacement en utilisant les 2 opérations.

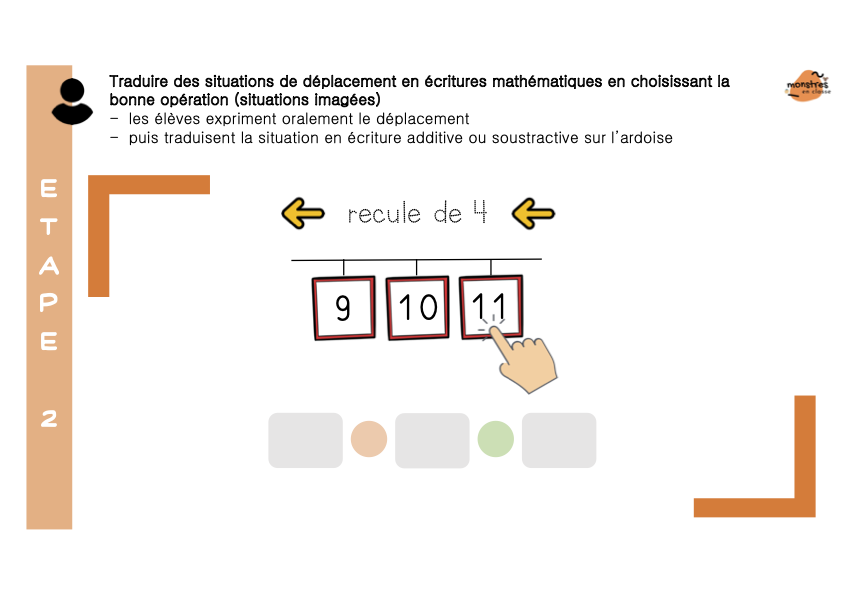
Dans l’étape suivante, les élèves découvrent les situations d’ajout et de retrait, et les traduisent là encore par les 2 opérations. Ils comprennent à nouveau qu’addition et soustraction sont équivalentes. Et commencent à résoudre des problèmes d’ajouts et de retraits : pas de priorité de l’ajout sur le retrait.
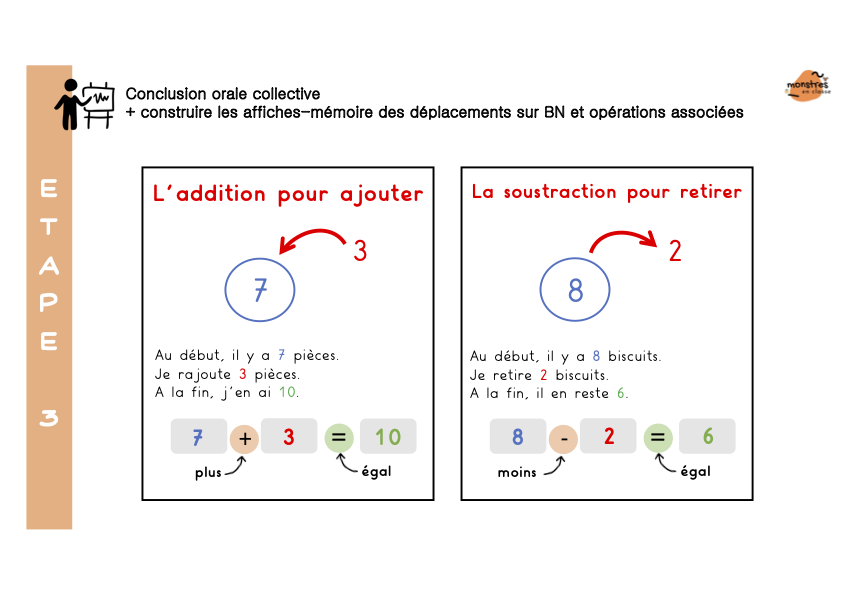
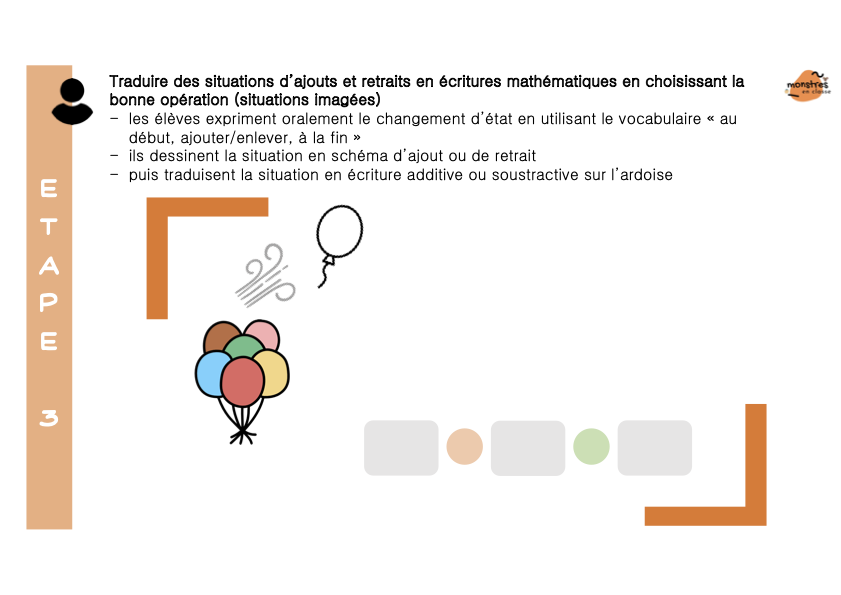
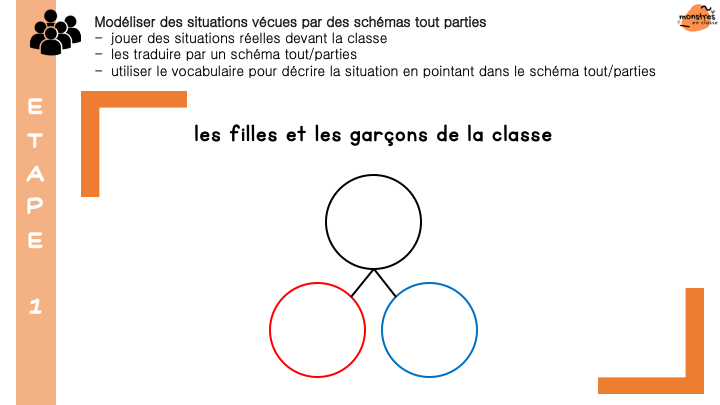
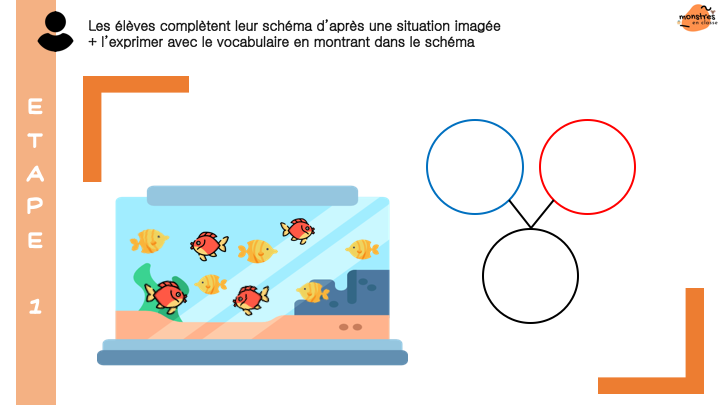
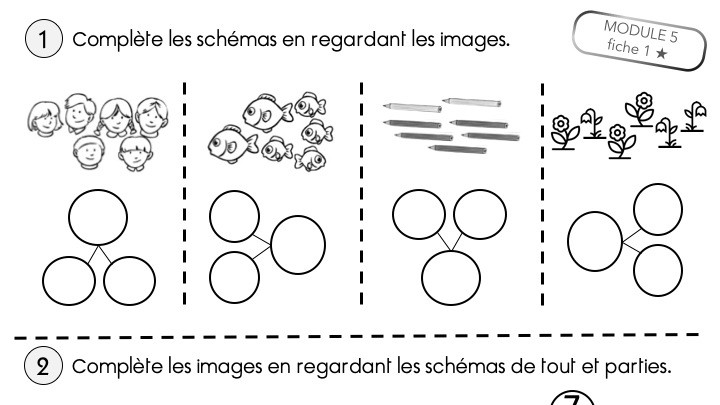
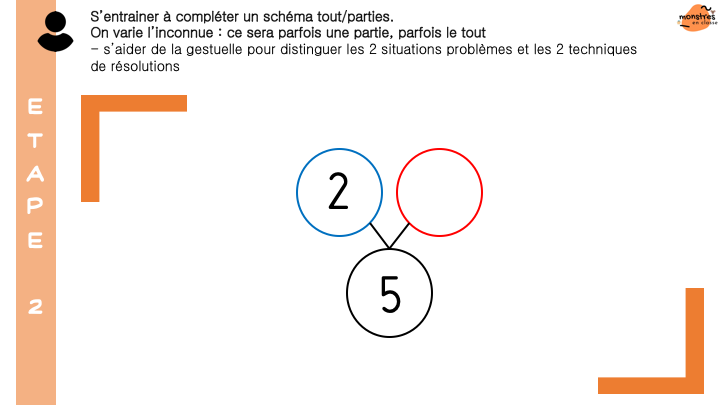
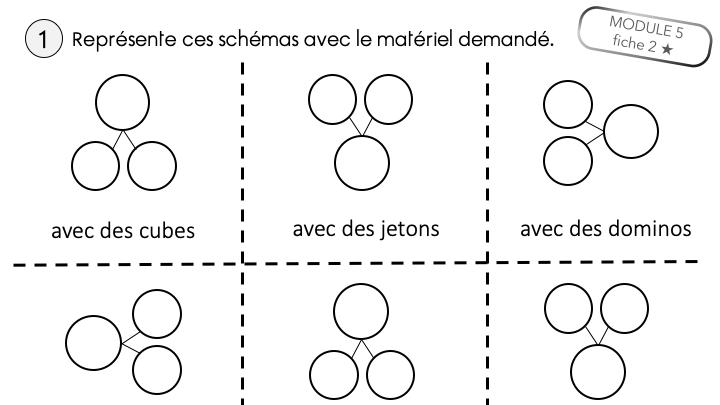
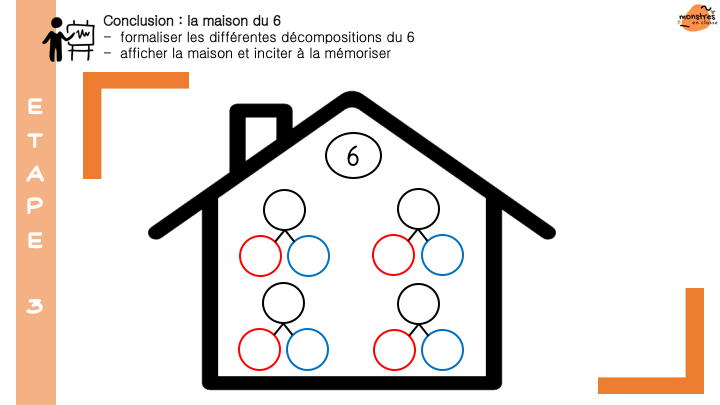
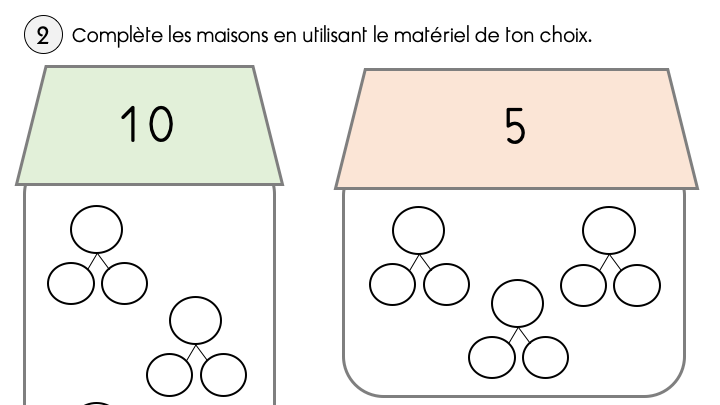
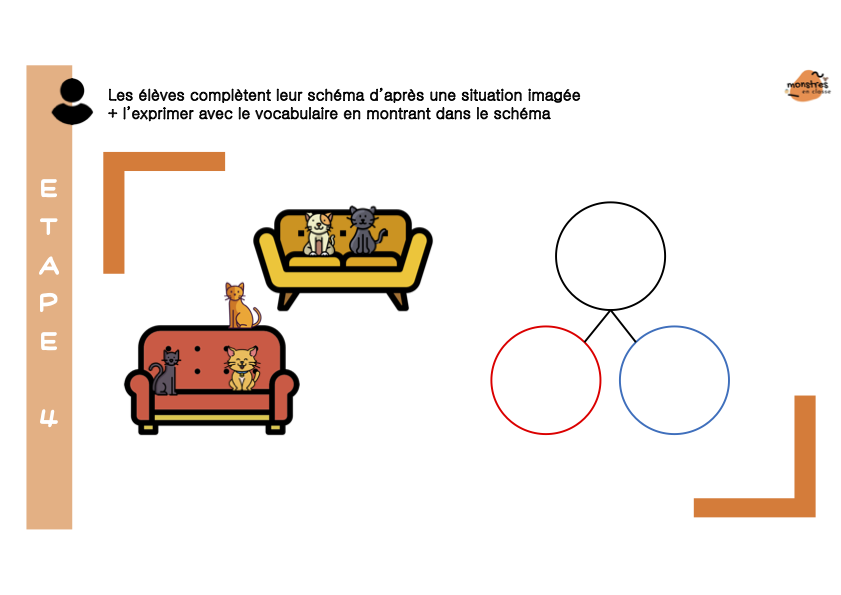
Enfin, (et c’est une grosse partie !) je présente les situations de tout et parties. D’abord les élèves s’approprient le concept de parties d’un tout et le schéma tout/parties à travers de multiples situations vécues en classes, imagées, évoquées. Puis ils s’entraînent à utiliser du matériel varié pour représenter des situations de tout et parties, puis pour résoudre des problèmes par la manipulation : rechercher le tout connaissant les parties, rechercher une partie connaissant le tout et l’autre partie.
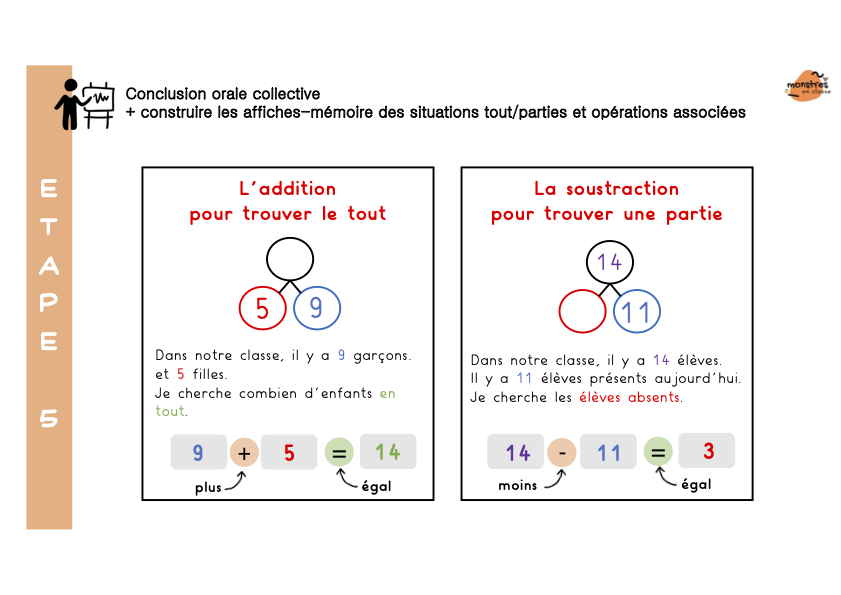
Enfin, ils découvrent comment l’addition permet de trouver le tout connaissant les parties, et comment la soustraction permet de trouver une partie inconnue.
Ce module est un gros module qui prend pas mal de temps, j’ai donc décidé cette année de le diviser en plusieurs morceaux afin de faire de la numération et de la géométrie entre les étapes, mais en gardant à l’esprit qu’addition et soustraction doivent être abordées simultanément et présentées comme des manières de traduire des situations concrètes. Les opérations doivent toujours avoir du sens, pour éviter le problème classique des élèves qui les emploient au hasard sans comprendre pourquoi lors de la résolution de problèmes.
Vous trouverez ici le diaporama avec le déroulé du module étape par étape:
Et ici les autres documents utiles :
Pour travailler le sens des opérations, j’ai crée ce jeu de cartes dans lequel les élèves traduisent une situation imagée ( de déplacement, d’ajout ou retrait, de recherche du tout ou d’une partie) par l’opération adéquate.
Mes sources :
Pour faire découvrir la notion d’égalité, j’utilise la balance du site Mathigon découvert grâce au super site de Classe à deux.
Les images utilisées ont du site Flaticon et certaines ont été empruntées à d’autres sites de partage : Nurvéro et Bout de gomme (si j’oublie qu’un, n’hésitez pas à me le signaler).
J’espère que ce partage vous plaira: j’ai mis longtemps pour arriver à cette manière de faire (et ça évoluera surement encore), alors si qq’un utilise et veut bien me donner son avis, ça me ferait plaisir.
Et surtout, n’hésitez pas à me signaler les erreurs, il y en a toujours qui résistent aux relectures.