Mathématiques

Module 8 : Les nombres jusque 69 + les nombres irréguliers de 11 à 16

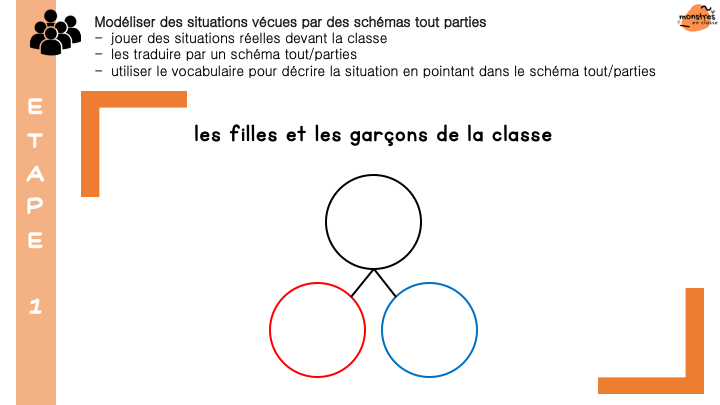
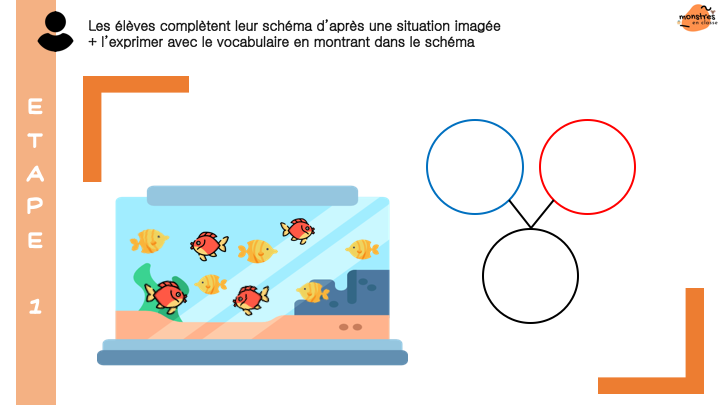
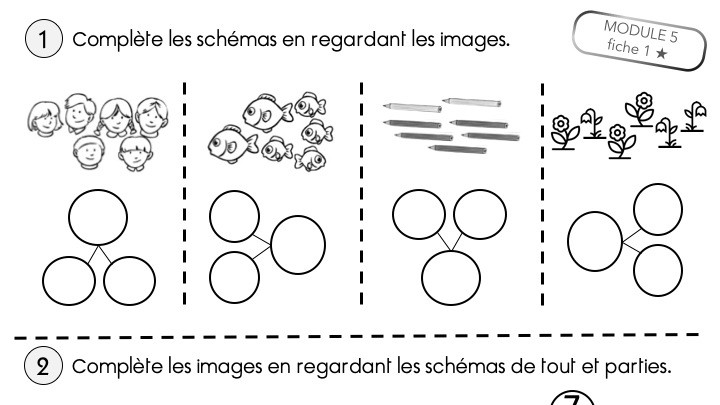
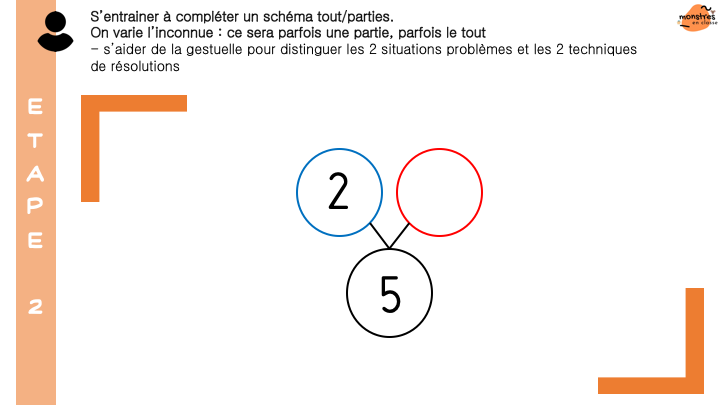
Découvrir et comprendre la numération jusqu’à 69:
– la notion de dizaine et d’unité
– dénombrer et constituer des collections
– la valeur positionnelle des chiffres dans un nombre
– l’irrégularité des nombres de 11 à 16


Mise à jour : Ce module a été revu en 2023, et se situe maintenant en 8ème module, au début de la période 3. Cela peut paraître tardif mais en réalité il ne sert qu’à structurer des apprentissages déjà initiés depuis le début de l’année dans le rituel du « Chaque jour compte » et à traiter en particulier le cas des irréguliers de 11 à 16.

Ce module s’appuie sur une vidéo disponible sur ma chaîne Youtube Les CP de Fontaine, que vous trouverez en cliquant ici.


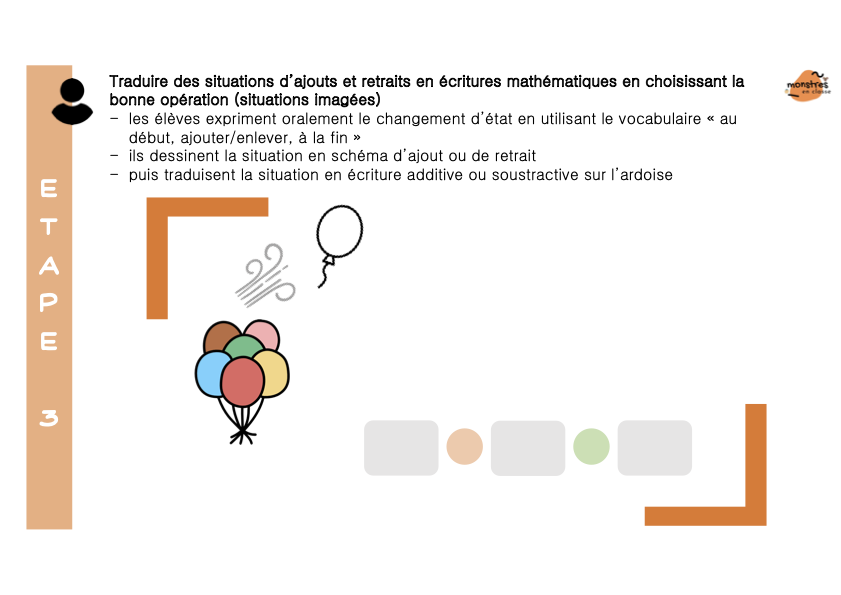
Dans un premier temps, je raconte « l’histoire de la numération » pour faire comprendre aux élèves ce qu’est la dizaine, et expliquer le principe du groupement par 10 qui régit notre numération.

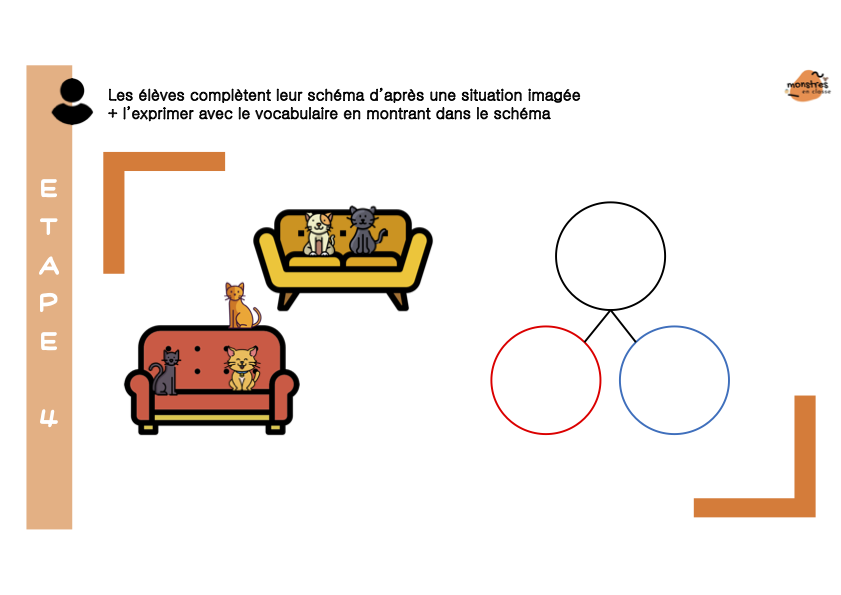
Ensuite, Les élèves travaillent sur des collections pour dénombrer et utiliser la désignation orale des nombres.

Puis je passe à l’écriture chiffrée, et donc à la valeur positionnelle des chiffres.

Et enfin, je traite le cas particulier des nombres irréguliers : je trouve très important d’apprendre aux élèves la désignation orale régulière de ces nombres :
« Douze est un nombre embêtant, normalement il devrait s’appeler dix-deux »
C’est cette étape qui leur évitera beaucoup de difficulté lorsqu’ils utiliseront les nombres des familles du 70 et 90.

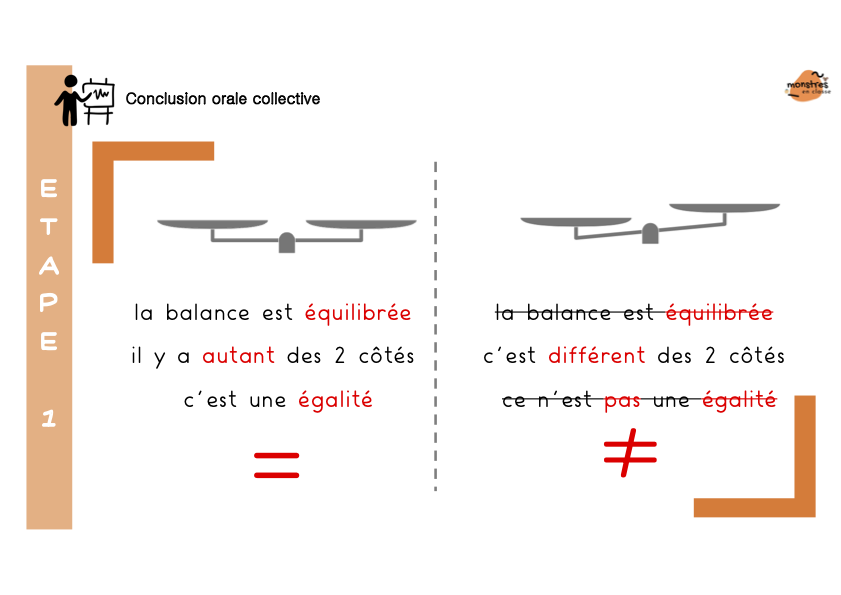
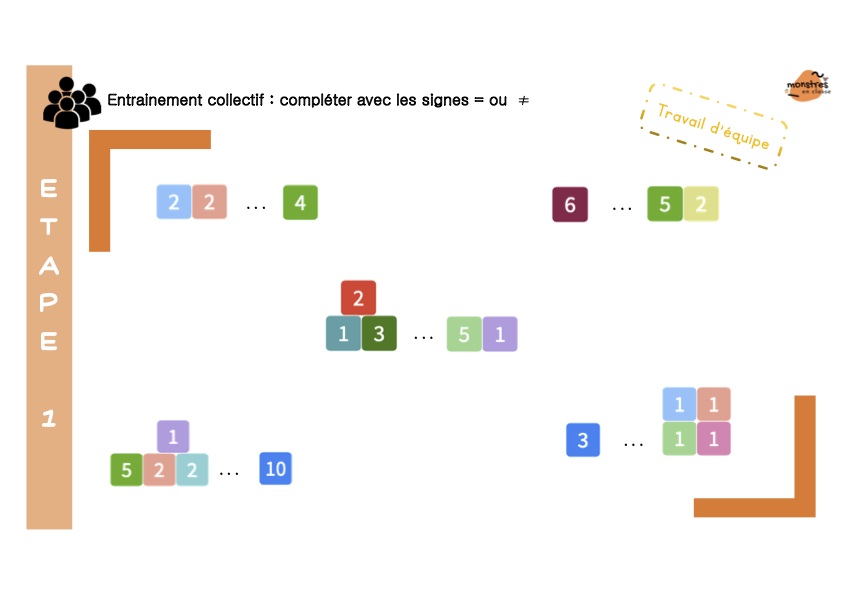
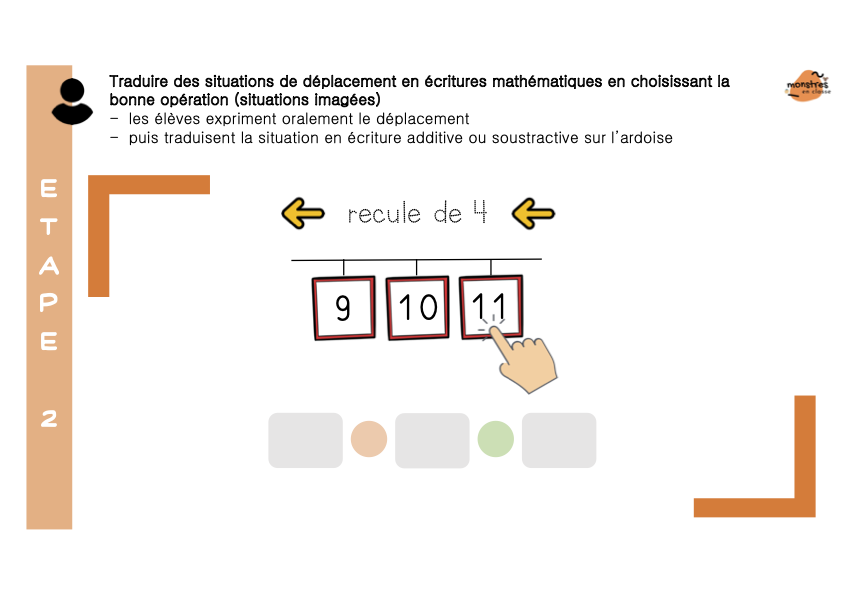
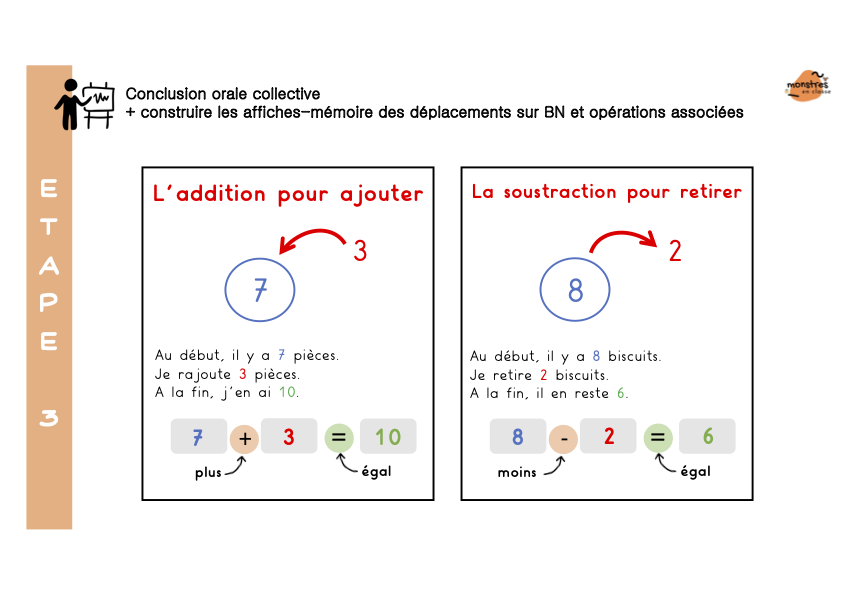
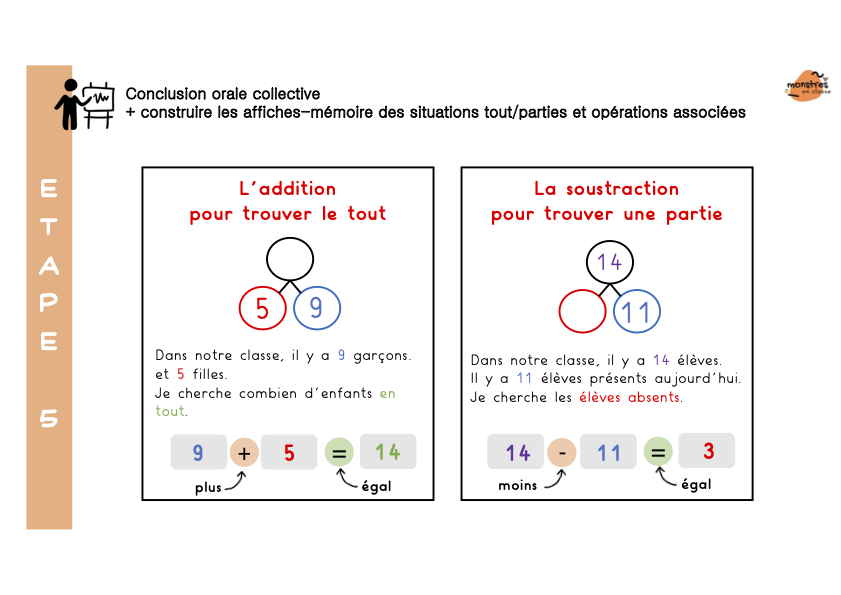
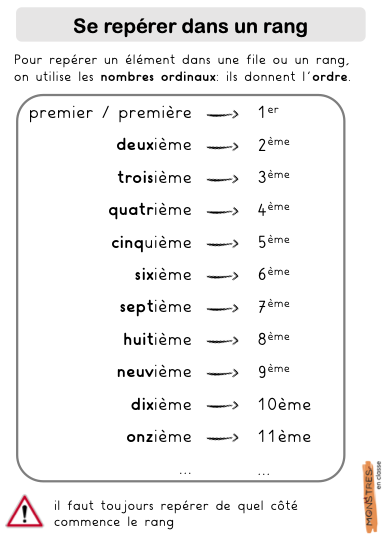
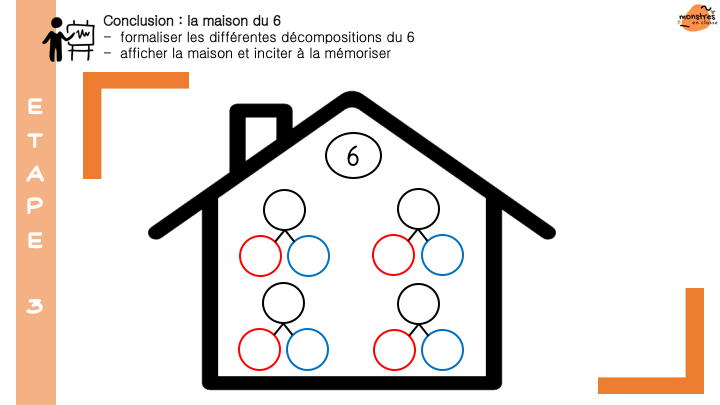
Les élèves colleront 4 minis leçons à mémoriser, et qui peuvent aussi servir d’affiches.

Voici le diaporama-déroulé du module qui me sert de fil conducteur pour tout le module:

Je veux voir


Et voici les différents documents utilisés :

les cartes Collections
le jeu du marchand
les fiches d’exercices
Les leçons

Le diapo contient des images du site Flaticon (dessinateurs : Freepik, Konkapp, AbdoCréative, Smashingstock, Smashicon, Iconhome, Wanicon, et vectorstall), et du site Edigo.

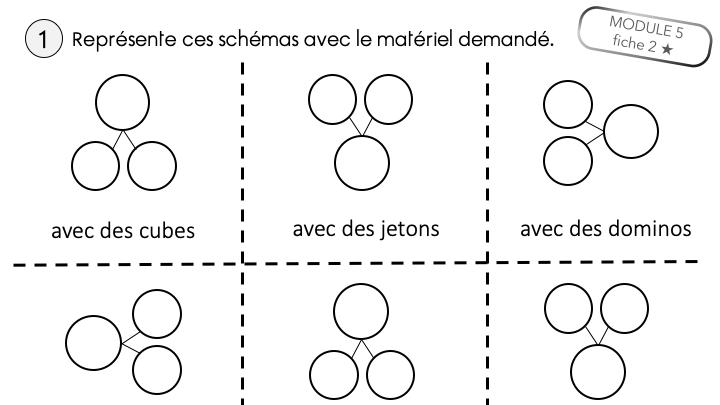
Pour mes fiches d’exercices, j’ai utilisé quelques images du site Flaticon également, ainsi que les images de Mysticlolly pour les représentations des nombres sur les doigts.
Comme d’habitude, chaque fiche est différenciée (cf les petites étoiles), et disponible en 2 versions pour que les voisins n’aient pas les mêmes données.

Dès que les notions sont découvertes en classe, je propose régulièrement des petites dictées et lecture de nombres, devinettes dizaine/unités, jeu du « J’ai, qui a? »

Comme d’habitude, n’hésitez pas à me donner vos avis et remarques, et surtout me prévenir d’éventuelles erreurs. Merci !

Module 6 : Le sens des opérations

Découvrir le sens des symboles = et ≠,
Comprendre et exprimer des situations de déplacement par des additions et soustractions,
Comprendre et exprimer des situations d’ajouts et retraits par des additions et soustractions,
Comprendre et exprimer des situations de tout et parties par des additions et soustractions,
Résoudre des problèmes mathématiques en reconnaissant la situation problème et en utilisant la bonne opération.


L’objectif principal est de faire découvrir l’addition et la soustraction comme 2 opérations mathématiques qui permettent de « raconter des histoires mathématiques » et donc de résoudre des problèmes mathématiques.

Dans un 1er temps, je présente les symboles = et ≠, et explique ce qu’est une égalité. Le symbole = n’est pas vu comme le signe d’un résultat mais bien comme le signe que les deux côtés de l’égalité représentent une valeur équivalente.

Ensuite, je présente les « histoires de déplacements en avant et en arrière », et j’introduis l’addition et la soustraction comme des opérations qui permettent de traduire en langage mathématique ces situations.
L’objectif est ici de présenter les 2 opérations en même temps, ainsi on ne donne pas de priorité à l’une ou l’autre, on ne prend pas le risque que les élèves s’habituent et privilégient l’addition car elle aura été abordée avant.

De plus, les opérations ainsi présentées sont comprises comme équivalentes : « avec l’addition, on avance, avec la soustraction, on recule. »
Les élèves commencent donc à résoudre des problèmes de déplacement en utilisant les 2 opérations.

Dans l’étape suivante, les élèves découvrent les situations d’ajout et de retrait, et les traduisent là encore par les 2 opérations. Ils comprennent à nouveau qu’addition et soustraction sont équivalentes. Et commencent à résoudre des problèmes d’ajouts et de retraits : pas de priorité de l’ajout sur le retrait.

Enfin, (et c’est une grosse partie !) je présente les situations de tout et parties. D’abord les élèves s’approprient le concept de parties d’un tout et le schéma tout/parties à travers de multiples situations vécues en classes, imagées, évoquées. Puis ils s’entraînent à utiliser du matériel varié pour représenter des situations de tout et parties, puis pour résoudre des problèmes par la manipulation : rechercher le tout connaissant les parties, rechercher une partie connaissant le tout et l’autre partie.
Enfin, ils découvrent comment l’addition permet de trouver le tout connaissant les parties, et comment la soustraction permet de trouver une partie inconnue.

Ce module est un gros module qui prend pas mal de temps, j’ai donc décidé cette année de le diviser en plusieurs morceaux afin de faire de la numération et de la géométrie entre les étapes, mais en gardant à l’esprit qu’addition et soustraction doivent être abordées simultanément et présentées comme des manières de traduire des situations concrètes. Les opérations doivent toujours avoir du sens, pour éviter le problème classique des élèves qui les emploient au hasard sans comprendre pourquoi lors de la résolution de problèmes.

Vous trouverez ici le diaporama avec le déroulé du module étape par étape:

Je veux voir

Et ici les autres documents utiles :

Les fiches d’exercices
Les affiches
Les schémas

Pour travailler le sens des opérations, j’ai crée ce jeu de cartes dans lequel les élèves traduisent une situation imagée ( de déplacement, d’ajout ou retrait, de recherche du tout ou d’une partie) par l’opération adéquate.

le jeu de cartes

Mes sources :
Pour faire découvrir la notion d’égalité, j’utilise la balance du site Mathigon découvert grâce au super site de Classe à deux.
Les images utilisées ont du site Flaticon et certaines ont été empruntées à d’autres sites de partage : Nurvéro et Bout de gomme (si j’oublie qu’un, n’hésitez pas à me le signaler).

J’espère que ce partage vous plaira: j’ai mis longtemps pour arriver à cette manière de faire (et ça évoluera surement encore), alors si qq’un utilise et veut bien me donner son avis, ça me ferait plaisir.
Et surtout, n’hésitez pas à me signaler les erreurs, il y en a toujours qui résistent aux relectures.

Module 4 : Les nombres ordinaux

Comprendre et utiliser les nombres ordinaux et leur formation,
Repérer un élément dans une file selon son rang,
Donner le rang d’un élément dans une file,
Faire le lien entre le rang et le nombre d’élément qui précèdent.

Mise à jour : Ce module a été revu en octobre 2022; dans la nouvelle progression, il prend la place du module 4.
Cette année (2022/2023) j’ai trouvé que les élèves ont eu beaucoup de mal avec ce module.

Ce module est destiné à la fin de la P1. Il est assez court et peut être traité rapidement.
En voici le diaporama du déroulé des séances de découverte et d’entrainement.

Je veux voir

Et voici la leçon, ainsi que les fiches d’exercices de fin de séquence.

la leçon
les fiches d’exercices

Comme d’habitude, les images utilisées viennent du site Flaticon, et du site Freepik. Merci aux dessinateurs.

Il ne reste plus qu’à trouver ou créer des jeux à faire en ateliers sur cette notion…
Si quelqu’un a ça, ou peut me recommander, je suis preneuse, et je ne manquerai pas de mettre un lien vers le site de l’auteur.

Si ce module vous plait, si vous repérez des erreurs, n’hésitez pas à laisser un commentaire. Merci !

Module 7 : Les tracés à la règle

Apprendre à utiliser la règle pour tracer des traits droits,
Relier des points et Reproduire des figures.

Mise à jour : Ce module a été revu, et le fichier d’entrainement remis en page. Dans la nouvelle progression, il est en module 7. Mais je pense qu’il peut être introduit assez tôt.

Tracer à la règle est une compétence qui nécessite surtout de l’entraînement, donc je me contente d’une présentation rapide des techniques et des erreurs à éviter, de quelques entraînements dirigés pour repérer les diffcultés et aider à mettre en oeuvre, puis je propose un petit fichier d’exercices que les élèves réalisent en ateliers du matin, une fois par semaine sur un temps assez long.
Généralement ce genre de petit fichier à réaliser seul leur plait beaucoup et les fait plutôt bien progresser.

Voilà donc le diaporama pour présenter les techniques et le petit fichier d’entraînement:

le diaporama-déroulé
le fichier d’exercice

NB : je ne relie pas ce petit fichier, les fiches sont juste regroupées dans une pochette, car pour les tracés à la règle, il vaut mieux un support bien à plat sur la table.


Les images du fichier d’exercice sont issues du site Flaticon et dessinées par Freepik, imaginationlol, berkahicon et eucalyp.

Si le fichier vous plait, un petit commentaire fait toujours plaisir.

ANCIEN Module 5 : Les situations tout/parties et les décompositions additives

Découvrir les situations de tout et de parties,
Résoudre des problèmes de tout/parties par la manipulation,
Construire le répertoire additif sous forme de décompositions tout/parties

Mise à jour : Ce module a été complètement révisé. Dans la nouvelle version, il y a d’abord un module de construction du sens des opérations, comme un langage pour raconter des situations (ajouts, retraits, déplacements, tout/parties), qui permet de résoudre des problèmes, les élèves s’entraînent à calculer. Et le répertoire additif est formalisé après.
Je ne sais pas encore quelle solution est la meilleure (ancienne ou nouvelle programmation), mais cette année (2022/2023), je regrette que le retard accumulé me fasse construire le répertoire trop tard. C’est dommage, mais il faut bien laisser aux élèves le temps dont ils ont besoin pour construire leurs savoirs.

Mon objectif principal dans ce module (et en général dans ma méthode de maths) est de construire les relations entre les nombres en partant de situations concrètes.
Je suis convaincue que les grandes difficultés que rencontrent nos élèves en calcul et surtout en résolution de problème viennent d’un manque de sens dans leur construction du nombre et du calcul.
Je veux qu’ils construisent les nombres et les opérations comme une « langue mathématique » qui sert à raconter des situations concrètes.
C’est pour cette raison que je construis les opérations assez tardivement, et que mes élèves s’entraînent à calculer et résoudre des problèmes avant de découvrir les opérations et les signes mathématiques.


Dans ce module, nous allons donc partir de situations concrètes de tout et de parties : des histoires. Nous allons d’abord apprendre à les schématiser, puis nous allons beaucoup manipuler pour représenter ces situations concrètes par divers matériels, et utiliser ce matériel pour résoudre des problèmes de tout et de parties.
Nous n’introduirons pas à ce stade ni l’addition, ni la soustraction.
Enfin, nous construirons le répertoire des décompositions additives des nombres jusqu’à 10, toujours en manipulant, et toujours sans utiliser l’écriture additive.

Etape 1 : Raconter, comprendre et schématiser des histoires de tout/parties

Etape 2 : Manipuler pour résoudre des problèmes de tout/parties

Etape 3 : Construire le répertoire des décompositions additives en manipulant

Comme d’habitude, voici le diaporama du déroulé complet du module, ainsi que les fiches d’exercices:

le diaporama-déroulé
les exercices


Pour faire ce module, vous aurez besoin des schémas individuels, des maisons pour construire les décompositions et de matériel varié, voici des idées:

– des cubes de plusieurs couleurs pour faire des tours, des trains
– le matériel pour construire des dominos
– des dés
– des gobelets et pailles ou bâtonnets
– des jetons et des petites boîtes
– des bracelets de perles sur du fil chenille
– des réglettes numériques

schémas tout/parties
maisons des décompositions
réglettes numériques
dominos manipulables

Les images de ce module viennent du site Flaticon, avec les dessinateurs : Freepik, GoodWare, victoruler, kalashnyk, Darius Dan, juicy fiche, icongeek26, ultimate arm, Vitalygorbachev, Didin jpr, Smashicons, DinosoftLabs, triberion, surang, AmesthysDesign et those icons ; d’autres visuels proviennent du site Edigo.

N’hésitez pas à commentez si vous avez un avis sur ce module, une proposition pour améliorer, ou juste me signaler une erreur.

Module 5 : Comparer, ranger et ajuster

Comparer et ajuster des collections en utilisant le vocabulaire plus/moins/autant,
Comparer et ranger les nombres entiers dans l’ordre croissant et décroissant

Mise à jour : Ce module a été revu en octobre 2022, et se situe maintenant en 5ème module, au début de la période 2.
Cette année (2022/2023) il est plutôt bien passé chez mes élèves.

Ce module se situe dans le champ numérique inférieur à 40. (Ce champ numérique évolue au rythme de l’atelier du matin « Chaque jour compte »)

Pour travailler la comparaison et rangement des nombres entiers, je pars d’abord du travail sur les collections.
Les élèves doivent être capables de comparer des collections (collections manipulables, collections imagées), pour cela il doivent être capables de comprendre et utiliser le vocabulaire PLUS/MOINS/AUTANT.
Ils doivent ensuite travailler sur ces collections : ajuster pour obtenir le cardinal demandé, ajuster pour avoir autant de plus / autant de moins.

Puis, la comparaison des nombres entiers vient comme moyen de comparer des collections que l’on ne peut pas manipuler, ou voir.
Ainsi cette notion n’est pas abstraite, la comparaison des nombres est bien liée à la comparaison de collections, et la notion d’ordre sur les nombres sera liée à la notion de comparaison des quantités.

Voici le diaporama-déroulé du module qui me sert de fil conducteur pour tout le module:

Je veux voir


Et voici les différents documents utilisés :

le jeu de bataille
le jeu des éventails
les fiches d’exercices
Les cartes ajustement de collections

Dans le diapo, je propose de découvrir le rangement dans l’ordre croissant/décroissant avec l’activité de Bout de Gomme, que vous trouverez ici : http://boutdegomme.fr/ateliers-numeration-ranger-les-nombres-en-cp-et-ce1

Le jeu de bataille est inspirée de Le stylo de Véro: je l’ai reconstruit en utilisant les images de Mysticlolly pour les représentations des nombres sur les doigts.

Le diapo contient des images du site Flaticon (dessinateurs : Freepik, victoruler, Kalashnyk, GoodWare, Darius Dan, juicy fich, icongeek26), et du site Edigo.

Pour mes fiches d’exercices, j’ai utilisé quelques images du site Flaticon également (dessinateurs : ibrandify, Freepik, kiranshastry, smashicons, True3 Art).
Comme d’habitude, chaque fiche est différenciée (cf les petites étoiles), et disponible en 2 versions pour que les voisins n’aient pas les mêmes données.

Dès que les notions sont découvertes en classe, je propose des jeux de comparaison, rangement, et ajustement, lors des mes ateliers du matin.

Comme d’habitude, n’hésitez pas à me donner vos avis et remarques, et surtout me prévenir d’éventuelles erreurs. Merci !

Module 3 : La monnaie

Découvrir les euros,
Dénombrer une somme,
Comparer des sommes,
Construire une somme pour payer

Mise à jour: Ce module a été revu et corrigé à l’été 2022, sans grandes modifications.
Merci de m’avertir si vous voyez des erreurs ou problèmes.

Ce module travaille la monnaie en restant dans un champ numérique inférieur à 20,
un autre module sur la monnaie est prévu en période 5.

Voici le diaporama-déroulé du module qui me sert de fil conducteur pour tout le module:

Je veux voir


Une grande partie du module se fait avec la vidéo que vous trouverez sur ma chaîne Youtube.
J’utilise cette vidéo en classe d’abord, puis les élèves la visionnent à nouveau à la maison avec leurs familles.
En voici le lien: https://youtu.be/PUasXrM96QI

Et voici les différents documents utilisés :

le jeu du marchand
la leçon
les fiches d’exercices


Le jeu du marchand contient des images du site Flaticon.

Pour mes fiches d’exercices, j’ai utilisé quelques images du site Flaticon également.
Comme d’habitude, chaque fiche est différenciée (cf les petites étoiles), et disponible en 2 versions pour que les voisins n’aient pas les mêmes données (cf la forme du bandeau de consigne).

Dès que ce module est démarré en classe, je propose des jeux sur la monnaie lors des mes ateliers du matin. Ainsi les élèves s’entraînent à dénombrer, comparer et constituer des sommes.

Vous trouverez plein de jeux très bien fait sur les sites des collègues-blogueurs.

Module 2 : Le repérage dans l’espace

Se repérer dans l’espace de la feuille,
Se repérer et repérer des positions dans l’espace,
Comprendre et utiliser le vocabulaire des positions relatives,
Distinguer la droite et la gauche sur soi et les autres

Mise à jour : module revu et corrige à l’été 2022, sans grandes modifications.
N’hésitez pas si vous trouvez des erreurs ou problèmes. Merci.

Dans ce module, les élèves travaillent beaucoup à l’oral.
Mon objectif est qu’ils comprennent et utilisent correctement le vocabulaire permettant de définir des positions.

Voici le diaporama-déroulé du module qui me sert de fil conducteur pour tout le module:

Je veux voir


Une grande partie du module se fait avec la vidéo que vous trouverez sur ma chaîne Youtube.
J’utilise cette vidéo en classe d’abord, puis les élèves la visionnent à nouveau à la maison avec leurs familles. (et j’espère qu’ils s’entraînent à utiliser le vocabulaire…)
En voici le lien: https://youtu.be/PUasXrM96QI

Et voici les différents documents utilisés :

le jeu: Quelle est ma carte?
les leçons
les fiches d’exercices

Pour la leçon sur le repérage dans l’espace feuille, je me suis inspirée de la leçon de Lutin Bazar dans son Mémo du CP chez Magnard.

Pour le travail sur la main droite/main gauche, je suis les propositions de Bout de gomme pour traiter cette notion super complexe.
Vous trouverez son travail ici : http://boutdegomme.fr/reperage-droite-et-gauche

Le jeu « Quelle est ma carte? » est inspiré de la méthode CapMaths.
Il permet de travailler la vocabulaire mais est aussi très intéressant pour découvrir des stratégies de déduction et de recherche par élimination.

Pour mes fiches d’exercices, j’ai utilisé les images du site Flaticon, et des dessinateurs : freepik, catkuro, kmg design, goodware, monkik, dinosoftLabs, xnimrodx et True3Art.
J’ai également repris quelques images issues du travail de Boutdegomme, et de la banque d’images LecturePlus.

Si j’ai oublié de citer des sources, n’hésitez pas à me le signaler, je corrigerai.

1er Module : Les nombres de 0 à 10, puis à 19…

La suite numérique orale jusqu’à 30,
Dénombrement jusqu’à 10 puis 19,
Les représentations des nombres de 0 à 10,
La suite numérique écrite jusqu’à 10, puis 19

Mise à jour : petit oubli signalé : la leçon des différentes représentations des nombres de 0 à 10 est ajoutée. (Merci Fabien)

Ce module, le premier de l’année, a pour objectifs:
– la connaissance de la suite numérique orale au moins jusqu’à 19
– la reconnaissance des écritures chiffrées jusqu’à 10
– les différentes représentations des nombres de 0 à 10
– le dénombrement et la construction de collections jusqu’à 10 (voire 19)
– la connaissance et la manipulation de la suite numérique orale et écrite jusqu’à 19

J’ai construit un diaporama-déroulé du module: c’est un fil conducteur à suivre page à page.
Ainsi, je n’ai plus besoin de retourner voir ma fiche de prep, je ne risque plus d’oublier des étapes, je peux faire des retours en arrière si besoin.
Et surtout les élèves sont acteurs de leur apprentissage : ils savent ce qu’ils vont apprendre dès le début du module, ils savent où ils en sont dans leur apprentissage, et comprennent simplement chaque étape du module du début à la fin.
Voici le diaporama-déroulé du module:

Je veux voir

Voici le matériel pour les différentes activités :

cartes à dénombrer
atelier Bandes numériques


Ajout récent : Voici d’autres cartes à dénombrer pour les élèves à l’aise : pour celles-ci, il y a 2 collections mélangées à dénombrer.

Cartes dénombrer 2 collections


Pour la construction des affiches des différentes représentations des nombres de 0 à 10, j’utilise le travail de Crapouilleries.net que vous trouverez ici : https://www.crapouilleries.net/article-ma-classe-affichage-des-nombres-jusqu-a-19-119617065.html (NB: personnellement, je n’exploite pas la représentation en petits bâtons)

Dans l’atelier sur les bandes numériques, j’utilise également les bandes numériques trouvées sur le site de Zaubette, et dont voici le lien : http://www.zaubette.fr/atelier-autonome-le-chiffre-manquant-ms-gs-a113036848

J’ai utilisé les bandes numériques de Bout de Gomme qui sont visuellement bien conçues pour passer de la bande à la droite numérique.

Et voici les fiches d’exercices,
– qui sont toutes en 2 versions avec des données différentes, ce qui permet de ne pas donner la même à 2 voisins, ou bien d’en faire une collectivement avant ou après la séance d’application en indiv. (on les distingue par le numéro 1 ou 1′ et la forme du bandeau.)
– et qui sont proposées avec difficulté croissante (1, 2 ou 3 étoiles): le plus souvent je propose la fiche 1 étoile à tout le monde, et les fiches suivantes sont données selon les capacités des élèves.
Cela me permet de travailler en 2 séances : 1ère séance: tout le monde démarre sur la fiche 1 étoile, et deuxième séance: un groupe dirigé pour continuer celle-ci pendant que les autres enchaînent sur les autres fiches.

Les fiches d’exercices

Et la leçon !

la leçon

Les images des représentations digitales et des constellations appartiennent à Mysticlolly, vous les trouverez sur son site ici.

Les élèves poursuivent le travail sur le dénombrement lors de ateliers de l’accueil, vous trouverez l’atelier complet ici: Atelier de dénombrement et manipulation de collections

Les cartes bandes numériques servent ensuite également lors des ateliers du matin, les élèves qui ont eu un peu de mal pendant le module ont alors le temps de s’entraîner plus longuement pour progresser.

Ma méthode de maths

Après quelques année pendant lesquelles j’ai utilisé des méthodes du commerce (CapMaths, La méthode de Singapour, Les maths avec Léonie), j’ai finalement décidé de me débrouiller toute seule en me servant de mon expérience.

J’essaie donc depuis deux trois ans maintenant de faire ma propre méthode de mathématiques qui correspond à mes élèves et mes façons de travailler.

Mise à jour:
Après une année de pratique, j’ai revu la programmation périodique, et mon organisation générale.
L’an prochain, ce sera :
– un rituel Chaque jour compte chaque matin,
– une séance quotidienne pour les modules d’apprentissage,
– une séance quotidienne de calcul mental et résolution de problèmes,
– + deux séances par semaine d’atelier pour s’entraîner et réinvestir,
– toujours, un diaporama fil conducteur pour chaque module,
– des vidéos pour apprendre et s’entraîner en classe et à la maison,
– des jeux et ateliers manipulables,
– des fiches d’exercices différenciés et de difficulté croissante pour chaque module,

La méthode est toujours en cours de construction, elle n’est pas encore totalement aboutie mais j’avance petit à petit, et je vais tenter de la partager au fur et à mesure.
Alors n’hésitez pas si vous avez des idées pour l’améliorer, ou s’il y a des erreurs à corriger…

Ici, vous trouverez la nouvelle programmation, la description des modules d’apprentissages et les activités en calcul mental par période:

la programmation
la description des modules
le calcul mental